WATANABE REN | 全国個人事業主支援協会

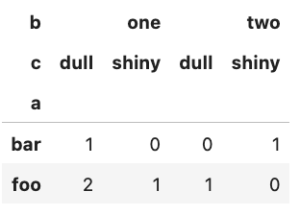
WATANABE REN wrote a new post, pandasのPivotについて④ 1年 10か月前

pivotメソッドの一般的なバージョン。

import datetime
df = pd.DataFrame(
   {
   “A”: [“one”, “one”, “two”, “three”] * 6,
   “B”: [“A”, “B”, “C”] * 8,
   “C”: [“foo”, “foo”, “foo”, “bar”, “bar”, “bar”] * 4[…]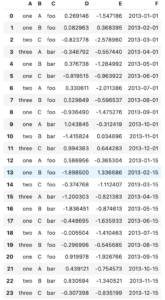

WATANABE REN wrote a new post, pandasのPivotについて③ 1年 10か月前

meltによるReshaping

unstackより柔軟性がある縦持ち方法。早めに知っておきたかった。

cheese = pd.DataFrame(
   {
       “first”: [“John”, “Mary”],
        “last”: [“Doe”, “Bo”],
        “height”: [5.5, 6.0],
        “weight”: [130, 150[…]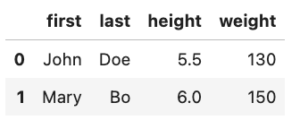

WATANABE REN wrote a new post, pandasのPivotについて② 1年 12か月前

列をMultiIndexとして格納するメソッドにstackがある。

tuples = list(zip(*[[“bar”, “bar”, “baz”, “baz”, “foo”, “foo”, “qux”, “qux”], [“one”, “two”, “one”, “two”, “one”, “two”, “one”, “two”],]))
index = pd.MultiIndex.f[…]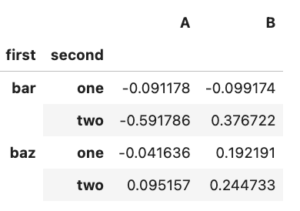

WATANABE REN wrote a new post, Pandas の pivotについて 2年前

軸ラベルを回転させてDataframeをもっと見やすくする。
Excelのピボットテーブルと同じ機能。
Dataframeに.pivotメソッドが用意されている。

def unpivot(frame):
“””
渡されたDFのIndexとColumnsを値とともに列方向に並べる。
“””
N, K = frame.shape
data = {
“value[…]

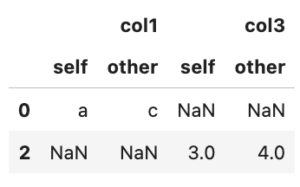
WATANABE REN wrote a new post, Pandas の compareについて 2年 1か月前

Pandasの標準搭載の比較メソッドとしてcompareがある。
df = pd.DataFrame(
{
“col1”: [“a”, “a”, “b”, “b”, “a”],
“col2”: [1.0, 2.0, 3.0, np.nan, 5.0],
“col3”: [1.0, 2.0, 3.0, 4.0, 5.0],
},
columns=[“col1”, “col2”, “[…]

WATANABE REN wrote a new post, PandasのMultiIndexについて⑧ 2年 2か月前

CategoricalIndex
種別系を扱う際に用意されているIndex Type。通常のSeriesへastypeで変換できる。

from pandas.api.types import CategoricalDtype

df = pd.DataFrame({“A”: np.arange(6), “B”: list(“aabbca”)})

df[“B”] = df[“B”].astype(Cat[…]

WATANABE REN wrote a new post, PandasのMultiIndexについて⑦ 2年 3か月前

takeメソッド
numpyでのIndexingによる抽出メソッドtakeを利用可能。locやilocよりも高速（但し、locほど柔軟性なし）

index = pd.Index(np.random.randint(0, 1000, 10))

positions = [0, 9, 3]

index[positions]

index.take(positions)[…]

WATANABE REN wrote a new post, PandasのMultiIndexについて⑥ 2年 4か月前

通常のIndexと同様sort_indexを用いてソートが可能

import random
random.shuffle(tuples)
s = pd.Series(np.random.randn(8), index=pd.MultiIndex.from_tuples([…]

WATANABE REN wrote a new post, PandasのMultiIndexについて⑤ 2年 5か月前

reindex レベルを跨いで値をブロードキャスト

midx = pd.MultiIndex(
levels=[[“zero”, “one”], [“x”, “y”]], codes=[[1, 1, 0, 0], [1, 0, 1, 0]]
)
df = pd.DataFrame(np.random.randn(4, 2), index=midx)
df2 = df.groupby(leve[…]

WATANABE REN wrote a new post, PandasのMultiIndexについて④ 2年 6か月前

Cross-section
xs()メソッドを使って、特定levelの要素を取得しやすくできる。idxを使用するよりさらに直感的。

df.xs(“one”, level=”second”)
df.xs(“bar”, level=”first”)

Sliceを用いるとこのような感じ

df.loc[(slice(None), “one”), :]

I[…]

WATANABE REN wrote a new post, PandasのMultiIndexについて③ 2年 7か月前

Slice

公式ドキュメント

セットアップ

miindex = pd.MultiIndex.from_product(
[mklbl(“A”, 4), mklbl(“B”, 2), mklbl(“C”, 4), mklbl(“D”, 2)]
)

micolumns = pd.MultiIndex.from_tuples(
[([…]

WATANABE REN wrote a new post, PandasのMultiIndexについて② 2年 9か月前

Basic Index
公式ドキュメントはこちら

①

通常のDataframeの列指定のように df[“label”] とすることで、該当するMultiIndexのレベルの階層を取得することが出来る。

サ[…]

WATANABE REN wrote a new post, PandasのMultiIndexについて① 2年 9か月前

MultiIndex
まずは公式ドキュメントから

①

arrays = [
[“bar”, “bar”, “baz”, “baz”, “foo”, “foo”, “qux”, “qux”],
[“one”, “two”, “one”, “two”, “one”, “two”, “one”, “two”],
]
tuples = list(zip(*arrays))
index =[…]

WATANABE REN wrote a new post, 統計・ファイナンス勉強ノート⑦ 2年 10か月前

ローレンツ曲線
・小さい値からXとYの累積相対度数を求め、表記したグラフ。完全な平等の場合の直線と比較して、観測値の不平等を確認する。

ジニ係数
・ローレンツ曲線と完全平等線の間の面積と、完全平等線以下の面積の割合。また、グラフ全体を一辺が1の正方形とすることで、ローレンツ曲線と完全平等線の間の面積の2倍と等しくなる。0~1の間をとり、大きければ大きいほど不平等な状態となっている。

移動平均
・時系列デー[…]

WATANABE REN wrote a new post, 統計・ファイナンス勉強ノート⑥ 2年 12か月前

回帰直線
・最小二乗法を用いて、観測値との差が最小になる直線

回帰平方和
・被説明変数の偏差の内、回帰直線を用いて計算される平方の総和

残差平方和
・被説明変数の偏差の内、回帰直線で計算結果からの残差の総和

総平方和
・偏差の平方の総和。回帰平方和と残差平方和を足した値

回帰直線における切片（α）と傾き（β）
・β：共分散/分散で計算できる
・α：被説明変数の平均 – β説明変数の平均[…]

WATANABE REN wrote a new post, 統計・ファイナンス勉強ノート⑤ 3年前

四分位数
・数の範囲を最小値、第一四分位数、中央値（第二四分位数）、第三四分位数、最大値に分ける